Ще докажем, че всички окръжности имат еднаква обиколка. Нека вземем две окръжности k₁ и k₂, които са с различни радиуси r₁<r₂ и с общ център O – представете си например страничния изглед на автомобилна гума и нейната джанта. Нека k₂ се допира до права (например гумата се допира до земята) в т.A₂ и нека OA₂ пресича k₁ в т.A₁.

Завъртаме окръжностите заедно така, че да направят цял оборот по правата (гумата се търкаля по земята). Очевидно точката от окръжността k₂, която преди се докосваше до земята в т.A₂ сега отново ще се докосва до правата, но в нова т.B₂. Ще забележите, че всички точки от окръжността k₂ в даден момент са се докосвали до отсечката A₂B₂. Следователно можем да твърдим, че дължината на A₂B₂ ще бъде периметъра на окръжността k₂.

Нека в новото положение OB₂ пресича k₁ в т.B₁. Очевидно можем да направим същите разсъждения за окръжност k₁ и отсечката A₁B₁ – всички точки на k₁ в даден момент от завъртането си са докосвали отсечката. Следователно дължината на A₁B₁ ще бъде равна на периметъра на окръжността k₁.

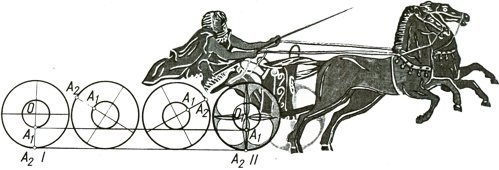
Да, но дължината на отсечката A₁B₁ e равна на дължината на отсечката A₂B₂. Следователно двете окръжности имат еднаква обиколка. Къде допускаме грешка?

Заблудата в задачата се получава от грешното заключение, че щом всяка точка от окръжността се е докосвала в даден момент до земята, то дължината на отсечката е равна на обиколката на окръжността – това е погрешно, защото гъстотата на точките е различна. Ако проследите траекторията на някоя точка от окръжността ще видите, че тя не е по права линия, а се движи по парабола.

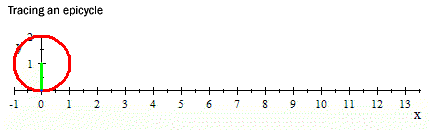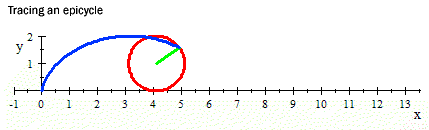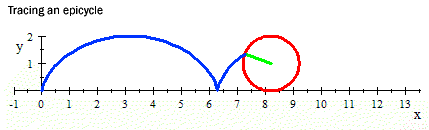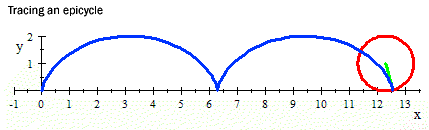
Източник на задачата и картинките: http://anadra.ru/sitemath/63.html