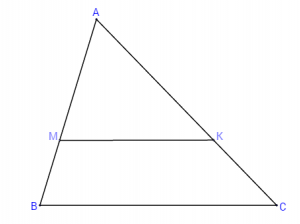
Нека в △ABC точка M лежи на страната AB и точка K лежи на страната AC така, че отсечката MK да е успоредна на BC. Лесно може да се докаже, че △ABC и △AMK са подобни, тоест е в сила пропорцията [latex]BC:MK = AB:AM[/latex]. От тук естествено следва, че:

$$BC.AM = MK.AB$$

Умножаваме двете страни на това равенство с [latex]BC – MK[/latex]:

$$BC.AM.(BC-MK) = MK.AB.(BC-MK)$$

$$\Rightarrow BC^{2}.AM-BC.AM.MK = BC.MK.AB-MK^{2}.AB$$

$$\Rightarrow BC^{2}.AM-BC.MK.AB = BC.AM.MK -MK^{2}.AB$$

$$\Rightarrow BC.(BC.AM-MK.AB) = MK.(BC.AM -MK.AB)$$

Съкращаваме двете страни на общия множител и получаваме:

$$BC = MK$$

С това доказахме, че всяка отсечка в триъгълника, успоредна на една от страните му, е равна на тази страна. От равенството [latex]BC.AM = MK.AB[/latex] лесно се вижда, че [latex]AM = AB[/latex], т.е. част от отсечка има дължина, равна на дължината на цялата отсечка. Къде допуснахме грешка в разсъжденията?

Като съкратихме двете страни на последното уравнение на общия множител [latex]BC.AM-MK.AB[/latex], премълчавайки, че този израз всъщност е равен на [latex]0 [/latex], умишлено нарушихме основно свойство на числовите равенства, а именно: Ако двете страни на едно уравнение се разделят или умножат с едно и също число, различно от нула, получава се уравнение, равносилно на даденото.
Тази задача е подходящ пример за упражнение на новите знания, усвоени в тема “Подобие” и същевременно за проверка на знанията за свойствата на числовите равенства.