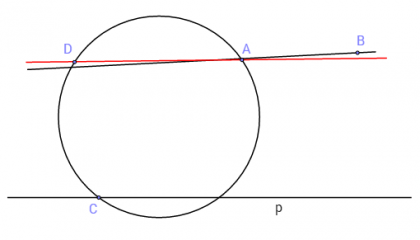
В равнината са дадени права p и точка A, нележаща на правата. През A прекарваме права q, успоредна на p. Избираме произволна точка C върху p и построяваме окръжност k с диаметър AC. Издигаме перпендикуляр към p в точка C и намираме неговата пресечна точка с окръжността k – нека това е точка D.

∢ADC=90, от което следва, че правата минаваща през точки A и D е успоредна на p. Но по условие q е успоредна на p, от което следва, че през точка A минават две прави, които са успоредни на p. Защо се получи така?

Грешката се дължи на чертежа и по-точно на приемането, че т.D е от окръжността k, но не лежи на правата q.
Така тази задача илюстрира колко важен е чертежът в построителните задачи. Само познаването и последователното прилагане на изучените свойства и теореми, биха осигурили достигането до коректност на чертежа, а от там и до вярно решение на всяка геометрична построителна задача.