Даден е тъп ∢ABD. От т. А издигаме перпендикуляр към AB, върху който нанасяме т. C такава, че AC=BD. Нека E и F са среди на отсечките AB и CD. Нека перпендикулярите от E към AB и от F към CD се пресичат в т. O. На първата фигура е показан случаят, когато т. O е извън четириъгълника ABCD:

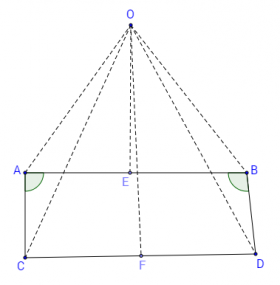
На втората фигура е даден случаят, когато т. O е вътре в четириъгълника ABCD:

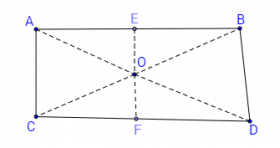
Понеже EO и FO са симетрали на AB и CD, то следва че AO=BO и DO=CO, а понеже по построение AC=BD, то от това следва, че △AOC и △BOD са еднакви. Следователно ∢OAC и ∢OBD са равни (1).

По аналогичен начин се доказва, че △AOE и △BOE също са еднакви, откъдето следва, че ∢OAE и ∢OBE са равни (2).

От (1) и (2) следва, че ∢CAB и ∢ABD са равни. Но по построение ∢CAB е прав, а по условие ∢ABD e тъп. Следователно тъпият ъгъл е прав!

Математическият софизъм в тази задача се дължи на неправилен чертеж. Конфигурациите по-горе са невъзможни. Действителната конфигурация е следната:

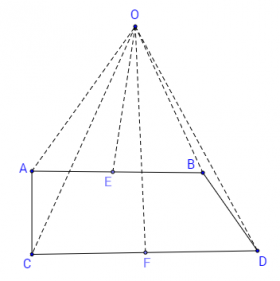
Лесно се вижда, че при тази конфигурация направените разсдъждения в “доказателството” са неверни. Подобни задачи са удачни за мотивиране на необходимостта от съставяне на точен чертеж.