Окръжност с два центъра
Нека е даден произволен ∢ABC. Върху раменете му избираме точки P и Q и от тях издигаме перпендикуляри съответно към AB и BC, които се пресичат в точка S. През точките P, Q и S описваме окръжност, която пресича AB в точка M и BC в точка N.
Знаем, че ∢MPS по построение е прав. Следователно MS е диаметър на окръжността. По същия начин знаем по построение, че ∢NQS е прав, откъдето следва, че NS също е диаметър на окръжността. Тогава средите на MS и NS – точки O1 и O2 – ще се явят два различни центъра на окръжността.
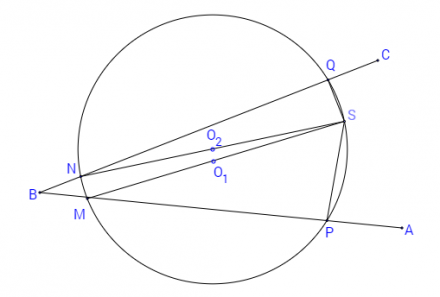
Софизмът в тази задача се дължи на пропускането на теоремата, която гласи, че “ако в изпъкнал четириъгълник, сборът на два срещуположни ъгъла е равен на 180 градуса, то около четириъгълника може да бъде описана (единствена) окръжност“. Ако се разгледа четириъгълникът BPSQ, се вижда, че двата срещуположни ъгъла ∢BPS и ∢BQS са прави, т.е. техният сбор е 180 градуса. Оттам следва, че окръжността трябва да премине през т.B, т.е. точки B, M и N съвпадат, а оттам съвпадат и O1 и O2.
No comments yet