Дадена е окръжност с център т.O и произволен диаметър AB. Избираме произволна т.M от окръжността (несъвпадаща с т.A и т.B) и прекарваме хордата AM. Нека т.P е среда на тази хорда, т.е. AP=PM. Нека правата BP пресича окръжността в т.N:

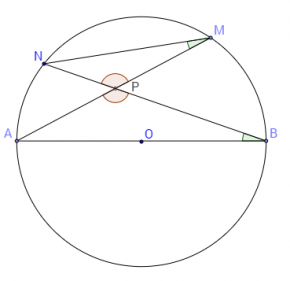
Разглеждаме △APB и △MNP:

1. ∢ABN=∢AMN (измерват се с една и съща дъга).
2. ∢APB=∢NPM (връхни)
3. AP=MP (по условие)

Следователно △APB и △MNP са еднакви. От тук следва, че AB=MN, т.е. хорда в окръжността е равна по дължина с диаметъра.

Заблудата в задачата произтича от това, че не е приложен валиден признак за еднаквост на триъгълници. Двата ъгъла не са прилежащи на равните страни, т.е. не е спазен втори признак за еднаквост на триъгълници.