Нов признак за еднаквост на триъгълници?
Знаете, че първи признак за еднаквост на триъгълници гласи: “два триъгълника са еднакви, ако две страни и ъгъл заключен между тях от единия триъгълник са съответно равни на две страни и ъгъл заключен между тях от другия”. Дали не е вярно и ако ъгълът НЕ е заключен между тях?
Дадени са △ABC и △PQR, които отговарят на условията:
- AB = PQ
- AC = PR
- ∢ACB = ∢PRQ
Преместваме △PQR така, че т.P да съвпада с т.А, т.B да съвпада с т.Q, а т.R и т.C да са от различни страни на правата AB. Нека новото положение на т.R да отбележим като т.D и нека т.E е пресечната точка на AB и CD. За т.E имаме три възможности:
- т.Е лежи вътре в отсечката AB:
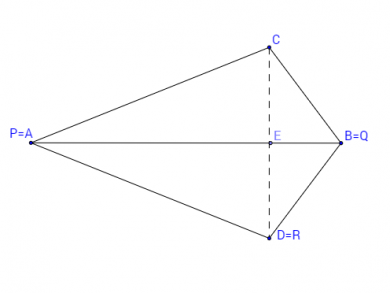
- т.Е лежи вдясно от т.B:
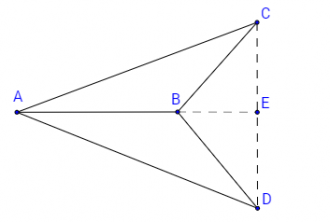
- т.Е лежи вляво от т.A:
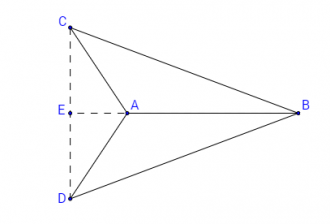
В първите два случая △ACD е равнобедрен, понеже по условие AC=PR=AD. Следователно ∢ADC = ∢ACD. Освен това по условие ∢ACB = ∢ADB. Чрез почленно изваждане ще получим, че ∢ECB = ∢EDB. Следователно △CBD e равнобедрен, т.е. BC = BD. Получихме, че и трите страни на △ABC и △PQR са равни, тоест триъгълниците са еднакви по трети признак. В случай 3 се работи аналогично.
Дали наистина получихме нов, четвърти признак за еднаквост на триъгълници? Какво пропускаме в “доказателството”?
При изучаване на признаците за еднаквост на триъгълници е съществено важно учениците да се научат да разпознават детайлите, които са отличителни за всеки един признак за еднаквост. В противен случай правилата стават наизустени, но не и разбрани. В частност това, че първи признак изисква ъгълът да е заключен задължително между двете равни страни, може лесно да се пропусне, което да доведе до съществени грешки при някои задачи. Затова е важно учителят да покаже контрапример, в който има триъгълници с две равни страни и равен ъгъл незаключен между тях, в който обаче пример триъгълниците всъщност са различни. Такъв пример е представен на следната фигура, където △CBD e равнобедрен:
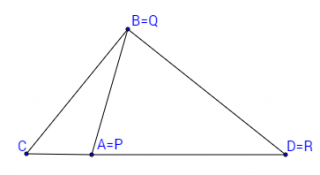
В показаната задача, чрез математическия софизъм можем да насочим учениците да помислят “дали наистина за т.E има три възможности”. Някои вероятно ще се досетят, че т.E може да съвпадне с т.A или т.B, откъдето впоследствие идват и частните случаи, в които този “четвърти признак” вече не е верен.
No comments yet