Нека разчертаем един голям квадрат в двора на училището, а после да го разграфим на по-малки квадрати. Долният ляв ъгъл на квадрата ще наречем т.А, а горният десен е т.B. Знаем, че най-късото разстояние от т.А до т.B е по права линия. Ако приемем, че страната на квадрата е равна на 1, то дължината на страната AB ще е [latex]\sqrt{2}[/latex]. На нас обаче ни е позволено да се движим от т.А до т.B само по линиите от мрежата, която сме направили. Един примерен път е показан на картинката по-долу:

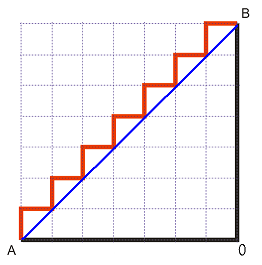
Може много лесно да се провери, че независимо по кой от пътищата с пунктир се движим, ние никога няма да стигнем от т.А до т.B за разстояние по-кратко от 2. От примера с картинката – няма значение дали се движим по червената или по черната линия, защото дължините им са равни. С други думи, дължината на червената линия е равна на сбора от катетите на △AOB.

Ние все пак ще се опитваме да се движим много близо до синята линия, която е най-късото възможно разстояние. Нека “наситним” мрежата и разграфим квадрата на още по-малки квадратчета:

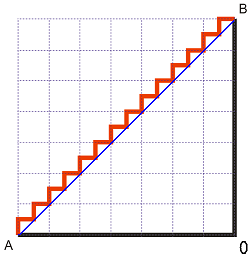
За съжаление и в този случай дължината на червената линия ще е 2. Ако опитаме с още по-малки квадратчета…

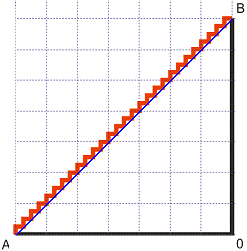
… дължината на червената линия ще продължава да е 2.

Но какво ще стане ако продължим да “наситняваме” мрежата ни до безкрайност? В един момент квадратчетата ще станат безкрайно малки, т.е. точки. А като станат точки, няма ли червената линия да съвпадне със синята, т.е. и тя да има дължина [latex]\sqrt{2}[/latex]? Но преди това казахме, че дължината на червената линия е равна на сбора от катетите на △AOB – значи получихме, че сборът на катетите на триъгълника е равен на неговата хипотенуза?!?

Задачата има много сходства с добре известните още от древността апории на Зенон. Заблудата в нея идва от приравняване на дискретно начупената червена линия към непрекъснатата синя. По същия начин Зенон приравнява дискретно времево към непрекъснато пространствено и непрекъснато времево към дискретно пространствено измерение и от там се получават познатите парадокси. Подобни задачи се очаква да насочат учениците към това да бъдат внимателни при работа с безкрайни множества.