π = 2
Нека е дадена окръжност с радиус r. Разделяме диаметъра на окръжността на n равни части. Всяка от получените отсечки използваме като диаметър за полуокръжност, така че да получим следната вълнообразна крива:
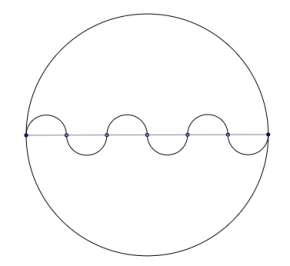
Знаем, че радиусът на всяка от получените полуокръжности е [latex]\frac{r}{n}[/latex], а дължината на всяка полуокръжност ще е [latex]\frac{\pi r}{n}[/latex]. Ако съберем дължините на всички полуокръжности ще получим:
$$n\frac{\pi r}{n}=\pi r$$
Виждаме, че дължината на вълнообразната линия не зависи от броя на деленията n.
Нека сега си представим, че броят на деленията нараства от n до безкрайност. Така диаметрите на полуокръжностите ще са безкрайно малки, т.е. ще бъдат точки, а от там и самите полуокръжности ще бъдат точки. Ще получим така, че дължината на вълнообразната крива ще съвпадне с диаметъра на голямата окръжност. Но ние знаем, че диаметърът на голямата окръжност е 2r, т.е. получаваме, че:
$$\pi r = 2r \Rightarrow \pi = 2$$
В задачата погрешно се приравнява дискретното деление на полуокръжностите с непрекъснатия диаметър. И тук може лесно да се направи препратка към апориите на Зенон.
Тази и други подобни задачи учат учениците, че сравнението между дискретни безкрайни редици и непрекъснати множества е неуместно.
No comments yet