Има един основен топологичен закон, който гласи, че две затворени криви, които се засичат, могат да бъдат разделени само ако едната от кривите се прекъсне. Например, не може да разделите верига без да прекъснете някоя от нейните брънки. Ако имате два зацепени един за друг пръстена, може да ги разделите само ако направите срез на един от двата. И т.н.

Нека имаме тор (това е геометрично тяло с формата на геврек, каквато е например вътрешната гума на велосипед). От вътрешната му страна е изчертана окръжност по неговия паралел, а по външната страна друга окръжност по неговия меридиан:

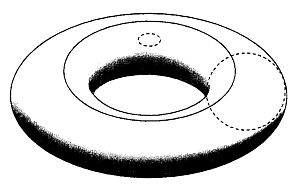
Очевидно е, че окръжността отвън ще бъде “зацепена” с тази отвътре – ако ги разгледаме само тях, те ще бъдат като две халки, които са вързани една за друга.

Нека сега пробием малка дупчица в тора и го обърнем наобратно – вътрешната страна да излезе отвън, а външната да влезе вътре. Това е показано на следната анимация:

Видимо е, че по този начин вътрешния пръстен ще излезе отвън, а външния ще влезе вътре. Да, но така те вече няма да са зацепени един за друг!

Решението на този софизъм е просто и идва непосредствено от изказването на закона от топологията. За да бъде обърнат тора наопаки е задължително окръжностите да бъдат прекъснати. Това е сложно да се докаже посредством математическо доказателство, но би могло да е интересно за възбуждане на въображението на учениците – да се опитат да си представят обръщането на тора (както е показано на анимацията) и да преценят къде точно става отрязването на окръжностите, което ги “отцепва” една от друга.