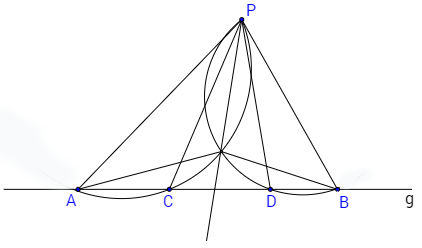
Нека е дадена права g и точка P вън от нея. Избираме точките A и B върху правата g, както е посочено на чертежа. Съединяваме P с A и B и върху отсечките AP и BP като върху диаметри построяваме полуокръжности, които пресичат правата g в точките C и D. Правите PC и PD са перпендикулярни на правата g, тъй като ∢ACP и ∢BDP са вписани в окръжности, а раменете им минават през краищата на диаметрите AP и BP, следователно са прави ъгли.

Така доказахме, че от т.P могат да се прекарат два перпендикуляра към правата g. Но нали не е възможно от една точка да се прекарат два различни перпендикуляра към една права?

Наистина, тъй като диаметрите AP и BP на двете окръжности по условие са различни, окръжностите се пресичат в т.P и т.Q. За т.Q има две възможности:
1) Q не лежи върху правата g;
2) Q лежи на правата g.
В разсъжденията сме приели, че е в сила 1) и тогава точките C и D са различни. В действителност е вярно 2).