Нека ABCD е квадрат, а PQRS е правоъгълник, който е вписан в него. Прекарваме правите QM и RN, които са успоредни на BC и AB, като т.M и т.N лежат съответно на страните CD и AD. Нека също т.O е пресечната точка на диагоналите на правоъгълника PQRS.

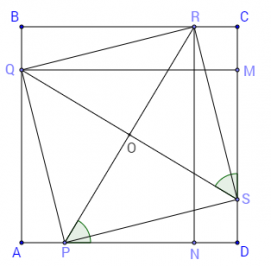
△QMS и △RNP са еднакви понеже:

1. И двата са правоъгълни
2. QM=BC = RN=AB
3. QS=RP (диагоналите на правоъгълника са равни)

Следователно ∢QSM = ∢RPN (1).

От това, че ∢OSD + ∢OSM = 180^o и (1) => ∢OSD + ∢RPN = 180^o  (2).

Сборът от ъглите на четириъгълника POSD е 360^o, т.е. от (2) => ∢PDS+ ∢POS = 180^o.

Но ние знаем, че по условие ∢PDS = 90^o, защото ABCD е квадрат. Следователно ∢POS = 90^o и от тук следва, че PQRS е квадрат, защото квадратът е единствения правоъгълник, чийто диагонали са перпендикулярни.

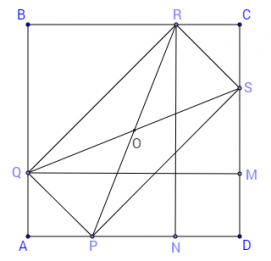
Софизмът в задачата се дължи на чертежа – разгледан е частен случай, в който PQRS действително е квадрат. Но това не е единствената възможна конфигурация. Приведените разсъждения са неприложими в случая, когато PQRS  не е квадрат. Тогава в конфигурацията, която принципно се различава от първата, т.M и т.D ще са от една и съща страна на т. S. Т.е. няма да бъде в сила равенството ∢OSD + ∢OSM = 180^o, което доведе до софизъм.