Нека в четириъгълника ABCD сумата от ъглите β и δ, съответно при върховете B и D, е β+δ=180^o (1)

През точките A, B и C описваме окръжност, която пресича страната AD в точка E. За ∢AEC=ε e в сила равенството β+ε=180^o (2)

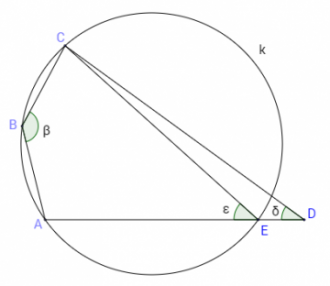
От (1) и (2) следва, че δ=ε. Следователно за △CDE следва, че външния ∢CEA е равен на несъседния нему вътрешен ∢CDE.

Математическата заблуда идва от погрешната постановка, че точки D и E не съвпадат. Учениците обикновено добре знаят теоремата, която гласи, че “ако изпъкнал четириъгълник е вписан в окръжност, сборът на негови два срещуположни ъгъла е равен на 180 градуса”. Трябва да се акцентира и върху обратната теорема, т.е. “ако в изпъкнал четириъгълник сборът на два срещуположни ъгъла е равен на 180 градуса, то около четириъгълника може да бъде описана (единствена) окръжност”. Именно от тази теорема следва, че т.D трябва да съвпадне с т.E.