Нека △ABC е правоъгълен с прав ъгъл в т.A. Нека O е пресечна точка на ъглополовящата BO на ∢ABC със симетралата QO на катета AC. Нека OR и OP са перпендикуляри към катета AB и хипотенузата BC:

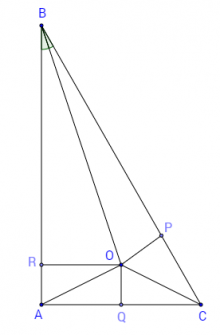
△OBR и △OBP са еднакви, понеже:

1. OB е обща хипотенуза
2. ∢BRO = ∢BPO = 90^o
3. ∢OBR = ∢OBP (BO е ъглополовяща)

Следователно BR = BP (1).

△ORA и △OPC също са еднакви, защото са правоъгълни и имат равни хипотенузи и равни катети (QO е симетрала на AC). Следователно RA = PC (2).

Ако съберем почленно (1) и (2), получаваме:

BR + RA = BP + PC

=> AB = BC

т.е. в △ABC катетът AB е равен на хипотенузата BC.

Аналогично се доказва, че AC = BC, от което следва, че правоъгълният триъгълник е равностранен. Къде допуснахме грешка?

Заблудата в тази задача се дължи на чертежа. Пресечната точка на ъглополовящата на остър ъгъл в правоъгълен триъгълник и симетралата на срещуположния на този ъгъл катет всъщност лежи извън триъгълника. Лесно може да се докаже, че пресечната точка лежи върху описаната около триъгълника окръжност:

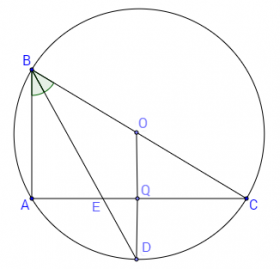
Наистина, нека ABC е произволен правоъгълен триъгълник. Описваме около него окръжност. Симетралата на катета AC разполовява дъгата AC в точка D. На ∢ABC съответства дъгата AC. Ако BE е ъглополовящата на този ъгъл, имаме ∢ABE=∢EBC. На тези ъгли отговарят равни дъги, понеже са вписани, откъдето следва, че ъглополовящата минава през точката D.