Дадена е координатна система и единична окръжност с център т.О. В окръжността е вписан правоъгълник HGFE, чийто страни са успоредни на координатните оси. Координатните оси пресичат страните на правоъгълника в точки M, N, L и K, както е показано на чертежа.

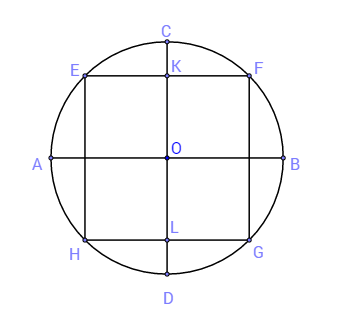
Известно е, че дължините, измервани в дясно от центъра на координатната система, в тригонометрията се считат за положителни, а в ляво от центъра – за отрицателни. Също така, разстоянията измервани над центъра по оста y, се приемат за положителни, а под центъра – за отрицателни. Вследствие на това може да се види лесно, че ON=-OM и OK=-OL. Следователно ON+OM=0 и OK+OL=0. Аналогично можем да видим, че OK+OL=0.

Тъй като ON=LG и OM=LH, то HL+LG=ON+OM=0. Аналогично се вижда, че FN+NG=0.

Лицето на правоъгълника EFGH = HG.GF. Да, но HG=HL+LG=0 и GF=FN+GN=0. Следователно и лицето на правоъгълника EFGH е равно на 0. Къде сбъркахме?

Уловката в задачата никак не е сложна и се очаква учениците лесно да я забележат, а именно: дължините на страните не могат да бъдат отрицателни числа. Можем да запишем |ON|=|-OM|, но не и ON=-OM.
Макар в задачата в явен вид да не присъстват тригонометрични функции, тя съдържа елементи, които се изучават в съответната тема. Това са координатната система и единичната окръжност. В тригонометричните задачи учениците често работят с отрицателни числа (например cos(π)=-1), ето защо някои от тях лесно могат да се подведат, че дължините на отсечките OA и OD (на чертежа) са равни на -1, а това не е вярно.
С тази задача може да се акцентира именно върху това, че трябва да се разграничават дължините на отсечките, получени при проекцията на раменете на ъгъла (те са винаги положителни числа!), от знака, с който бележим посоката на вектора, който от своя страна зависи от квадранта, в който попада ъгълът.