Даден е △ABC с ъгли в съответните точки α, β и γ. Нека страните AB=c и AC=b. Продължете отсечката BA до т.М така, че AM=b, а отсечката CA до точка K така, че AK=c.

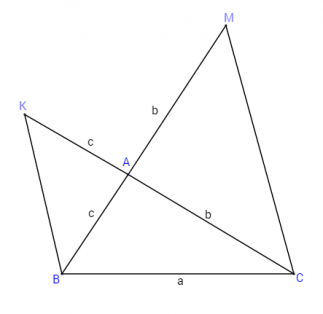
Да приложим синусовата теорема за △BCK и △BCM:

$$\sin{\left(\beta+\frac{1}{2}\alpha\right)} = \frac{b+c}{a}.\sin{\frac{1}{2}\alpha}$$

$$\sin{\left(\gamma+\frac{1}{2}\alpha\right)} = \frac{b+c}{a}.\sin{\frac{1}{2}\alpha}$$

$$\Rightarrow \sin{\left(\beta+\frac{1}{2}\alpha\right)} = \sin{\left(\gamma+\frac{1}{2}\alpha\right)} \Rightarrow \beta+\frac{\alpha}{2} = \gamma+\frac{\alpha}{2} \Rightarrow \beta = \gamma$$

Аналогично се доказва, че и [latex]\gamma = \alpha[/latex]. Следователно трите ъгъла на триъгълника са равни, т.е. той е равностранен.

Обяснението на този софизъм се състои в това, че от [latex]sin{(x)} = sin{(y)}[/latex], не следва непременно, че [latex]x=y[/latex]. От периодичността на функциията [latex]sin[/latex], всъщност следва зависимостта:
$$x=\left(-1\right)^{k}y+k.180^{\circ}, \left(k=0,\pm1,\pm2,…\right)$$

Според горната формула при [latex]к=0[/latex] се достига до частния случай, към който ни подвежда софизмът в задачата:
$$\beta+\frac{\alpha}{2} = \left(-1\right)^{0}\left(\gamma+\frac{\alpha}{2}\right)+0.180^{\circ} \Rightarrow \beta+\frac{\alpha}{2} = \gamma+\frac{\alpha}{2} \Rightarrow \beta = \gamma$$

В разглеждания случай обаче следва да се съобрази, че [latex]\alpha+\beta+\gamma = 180^{\circ}[/latex].
Тогава решение на задачата има само при [latex]k=1[/latex]:
$$\sin{\left(\beta+\frac{1}{2}\alpha\right)} = \sin{\left(\gamma+\frac{1}{2}\alpha\right)} \Rightarrow \beta+\frac{\alpha}{2} = -\left(\gamma+\frac{\alpha}{2}\right)+180^{\circ} \Rightarrow \alpha+\beta+\gamma = 180^{\circ}$$