Никои две прави в една равнина не се пресичат
Нека g и h са две различни прави в една равнина. Нека т.A е от g, а т.B е от h. Построяваме точки A1 и B1 такива, че:
$$AA_{1} = BB_{1} = \frac{AB}{2}$$
Отсечките AA1 и BB1 не се пресичат, защото в противен случай ще се получи следната фигура:
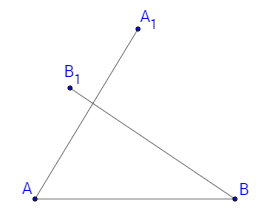
от която следва, че:
$$AC+BC < AA_{1} + BB_{1} = AB$$
А това очевидно не е вярно, защото в един триъгълник сборът на кои да е две страни е винаги по-голям от третата.
Построяваме точки A2 и B2 такива, че:
$$A_{1}A_{2} = B_{1}B_{2} = \frac{A_{1}B_{1}}{2}$$
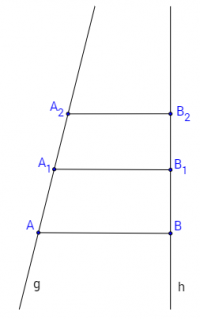
По съображения, подобни на изложените по-горе, можем да заключим, че отсечките A1A2 и B1B2 също не се пресичат. Този процес може да продължи до безкрайност. Следователно правите g и h не се пресичат, а те бяха произволно избрани. Следователно, никои две различни прави в една равнина не се пресичат, или което е същото: всички прави в една равнина са успоредни.
Задачата е известна като “Софизмът на Прокъл”. Доказателството, че AA1 и BB1 не се пресичат, A1A2 и B1B2 не се пресичат и т.н., е безупречно, но от това не следва, че g и h не се пресичат, защото е напълно възможно AA1 да пресича например B1B2.
No comments yet