Всеки триъгълник е правоъгълен
Даден е △ABC с ъгли α, β и γ. Нека CD=h е височината към AB през т.C. Нека AB=c, AC=b, BC=a, AD=m и BD=n.
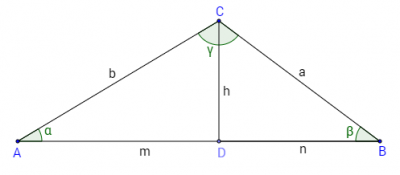
При тези означения е вярно, че:
$$(1) \quad \sin{(\alpha + \beta)} = \sin{(\alpha)}\cos{(\beta)} + \cos{(\alpha)} \sin{(\beta)} = \\ = \frac{h}{b} \frac{n}{a} +\frac{m}{b} \frac{h}{a} = \frac{h}{ab} (m+n) = \frac{hc}{ab}$$
Ако R е радиусът на описаната около △ABC окръжност, то:
$$(2) \quad a=2R\sin{(\alpha)}, b=2R\sin{(\beta)}, c=2R\sin{(\gamma)}$$
От тук може да изразим:
$$(3) \quad h=b\sin{(\alpha)}=2R\sin{(\alpha)}\sin{(\beta)}$$
Заместваме изразите за a, b, c и h от (2) и (3) в (1):
$$sin{(\alpha+\beta)} = sin{(\gamma)} \Rightarrow \alpha+\beta=\gamma$$
Но понеже α+β+γ=180o, то следва че:
$$\gamma = 90^{o}$$
Софизмът в тази задача се получава от това, че от [latex]sin{(\alpha+\beta)} = sin{(\gamma)}[/latex] не следва непременно, че [latex]\alpha+\beta=\gamma[/latex].
Подходящо е задачата да се реши заедно с учениците, след като вече е усвоен материалът за периодичност на тригонометричните функции – от една страна за проверка до колко са усвоени тези знания и от друга – за затвърждаване на материала.
No comments yet