Нека вземем сфера и начертаем меридиани (по аналогия с меридианите от земното кълбо). Ще се получи следното:

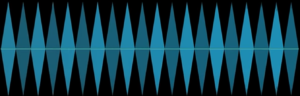
Сега нека ги разгънем (да обелим сферата подобно на обелването на кора на плод):

От тези ленти с триъгълници ще можем да сглобим един успоредник:

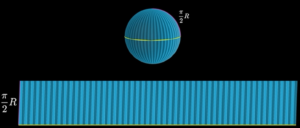
При това ще забележите, че долната страна на успоредника ще е равна на обиколката на сферата при нейния екватор, а страната му ще е дъгата от екватора до северния полюс. Ако радиусът на сферата е [latex]R[/latex], то тогава страните ще са [latex]2 \pi R[/latex] и [latex]\frac{\pi}{2}R[/latex].

По този начин лицето на развивката, което е и лице на сферата изглежда, че е зависимо от ъгъла в успоредника. Ако ние разрязваме сферата на по-малки и по-малки парченца, нейната развивка ще започне все повече да изглежда като правоъгълник:

Получават се две изключително странни явления:

1. Лицето на сферата се мени в зависимост от това как сме я разрязали;
2. При най-финото разрязване (представете си, че триъгълниците стават безкрайно много – тогава фигурата наистина ще се изправи в правоъгълник) нейното лице ще бъде [latex]S=2 \pi R \frac{\pi}{2}R = \pi^{2}R^{2}[/latex], което е точно четири пъти (!) по-малко от добре познатата ви формула за лице на сфера…

Задачата е взета от 3Blue1Brown.

Уловката идва от там, че подвеждаме учениците, че развивката е от триъгълници. Всъщност страните на всеки „триъгълник“ са криви:

Разликата се натрупва във всеки от тях и това довежда до значителна грешка.

Задачата изисква познания за повърхнина на сфера, която се изучава в VI клас, но за съжаление включва и измерване на дължина на дъга на окръжност, която се изучава в VIII клас. За щастие тук използваната дъга е лесно да се забележи, че е точно една четвърт от обиколката на сферата, т.е. знаейки колко е обиколката на окръжност, учениците биха могли да пресметнат лесно 1/4 от нея. Включваме задачата и в раздел „окръжност“ за VIII клас, защото би могла да се използва като препратка за опресняване на стари знания, с които да се разнообрази темата.